Polynomial Eqn Solving with BF FDG and SF: Easy Ways to Solve Equations

Polynomial eqn solving with BF FDG and SF might sound complicated, but it can be quite simple! These methods help us solve polynomial equations in a step-by-step way. You can think of them like tools in a toolbox, each one doing something special to solve math problems.

In polynomial eqn solving with BF FDG and SF, we use these tools to find answers to equations that have lots of terms, like x² + 3x + 2. By using BF (Brute Force), FDG (Finite Difference Gradient), and SF (Successive Filtering), we can make the problem easier to understand and solve. Let’s explore how each method works and see some examples!

Introduction to Polynomial Eqn Solving with BF FDG and SF

Polynomial equations can seem tricky at first, but they’re just a way of writing math problems with variables raised to different powers. For example, x2+2x+1=0x^2 + 2x + 1 = 0x2+2x+1=0 is a polynomial equation. Solving these equations is important in many fields, from engineering to computer science. To make solving polynomials easier, we use different methods, including BF (Brute Force), FDG (Factorization), and SF (Substitution and Factoring).

Brute Force (BF) is like trying out different solutions until you find the right one. Factorization (FDG) involves breaking down the polynomial into simpler parts. Substitution and Factoring (SF) means replacing parts of the polynomial with simpler expressions to make solving easier. Each method has its own way of tackling polynomial equations, and knowing when to use each one can help you solve problems more efficiently. In this blog post, we will explore these methods in detail and see how they can be applied to solve polynomial equations.

Understanding these techniques will make you more confident in handling polynomials, whether you’re solving them for homework, projects, or just for fun.

What Does Polynomial Eqn Solving with BF FDG and SF Mean?

When we talk about polynomial equations, we’re referring to equations where variables are raised to powers. For example, 3×2+5x−2=03x^2 + 5x – 2 = 03×2+5x−2=0 is a polynomial equation. Solving these equations helps us find the values of the variables that make the equation true.

BF stands for Brute Force. This method involves testing various possible solutions until you find one that works. It’s a straightforward approach but can be time-consuming for complex equations. FDG stands for Factorization. This technique involves breaking down the polynomial into simpler factors, which makes it easier to find solutions. SF stands for Substitution and Factoring. This method involves substituting parts of the polynomial with simpler expressions to make the equation easier to solve.

By understanding these methods, you can choose the best approach to solve different polynomial equations. In the following sections, we will look at each method in detail to help you understand how they work and when to use them.

Basics of Polynomial Equations for Beginners

Polynomial equations might sound complicated, but they’re built from simple concepts. A polynomial is a math expression made up of variables and constants combined using addition, subtraction, and multiplication. For example, 2×3+3×2−x+52x^3 + 3x^2 – x + 52×3+3×2−x+5 is a polynomial. The highest power of the variable xxx is called the degree of the polynomial.

This means we need to solve for xxx in an equation like 2×2−4=02x^2 – 4 = 02×2−4=0. The methods we use, such as Brute Force, Factorization, and Substitution and Factoring, help us find these values by simplifying the equation in different ways.

Understanding the basics of polynomials is the first step in learning how to solve them. Once you know what polynomials are and how they work, you can start applying different methods to solve them. 

How Brute Force (BF) Helps in Polynomial Eqn Solving

Brute Force (BF) is one of the simplest ways to solve polynomial equations. The BF method involves trying out different values for the variable until you find one that works. It’s like guessing the answer and checking if it’s correct.

For example, if you have an equation like x2−4=0x^2 – 4 = 0x2−4=0, you might try different values for xxx like 1, 2, 3, etc. You check each value to see if it satisfies the equation. If you try x=2x = 2x=2, you get 22−4=02^2 – 4 = 022−4=0, which is correct. So, x=2x = 2x=2 is a solution.

BF can be useful for simple equations where you can easily test different values. However, it can be time-consuming for more complex polynomials with many possible solutions. Despite its simplicity, BF provides a basic understanding of how solutions to polynomial equations are found.

Step-by-Step Guide to Using BF in Polynomial Eqn Solving

Using the Brute Force (BF) method involves a few simple steps. First, write down your polynomial equation and decide which values to test. For example, if your equation is x2−3x+2=0x^2 – 3x + 2 = 0x2−3x+2=0, you start by guessing different values for xxx.

Next, substitute each value into the equation to see if it works. For x=1x = 1x=1, substitute it into the equation: 12−3(1)+2=01^2 – 3(1) + 2 = 012−3(1)+2=0. This simplifies to 1−3+2=01 – 3 + 2 = 01−3+2=0, which is true. So, x=1x = 1x=1 is a solution.

Continue testing other values if needed. This method works best for simpler equations where you can easily test a few values. For more complex equations, BF might not be practical, and other methods might be necessary. But for beginners, BF is a great way to start understanding how solutions are found.

Understanding Factorization in Polynomial Eqn Solving with FDG

Factorization (FDG) is a method used to simplify and solve polynomial equations by breaking them down into simpler parts. The idea is to express the polynomial as a product of its factors. For example, the polynomial x2−5x+6x^2 – 5x + 6×2−5x+6 can be factored into (x−2)(x−3)(x – 2)(x – 3)(x−2)(x−3).

To factor a polynomial, look for two numbers that multiply to give the constant term and add up to give the coefficient of the middle term. In the example above, -2 and -3 are the numbers that work. Once you factor the polynomial, you can solve it by setting each factor equal to zero: x−2=0x – 2 = 0x−2=0 and x−3=0x – 3 = 0x−3=0. This gives the solutions x=2x = 2x=2 and x=3x = 3x=3.

Factorization makes solving polynomials easier by breaking them down into simpler equations. It’s a useful method when dealing with quadratic polynomials and can be extended to more complex cases with higher-degree polynomials.

How FDG Simplifies Polynomial Equations

Factorization (FDG) simplifies polynomial equations by breaking them into simpler factors. When you factor a polynomial, you rewrite it as a product of simpler expressions. This makes it easier to solve because you can find the roots of these simpler expressions.

For example, if you have the polynomial x3−6×2+11x−6x^3 – 6x^2 + 11x – 6×3−6×2+11x−6, you can factor it into (x−1)(x−2)(x−3)(x – 1)(x – 2)(x – 3)(x−1)(x−2)(x−3). By setting each factor equal to zero, you can find the solutions: x=1x = 1x=1, x=2x = 2x=2, and x=3x = 3x=3. This process of factoring simplifies the equation and makes it easier to solve.

Factorization is especially helpful for quadratic and cubic polynomials. By breaking them down into simpler factors, you can solve them more efficiently. This method reduces the complexity of the polynomial and allows you to find the solutions more quickly.

Practical Examples of FDG in Polynomial Eqn Solving

Let’s look at a practical example of using Factorization (FDG) to solve a polynomial equation. Suppose you have the polynomial x2−7x+10x^2 – 7x + 10×2−7x+10. To solve it using FDG, first factor the polynomial into (x−2)(x−5)(x – 2)(x – 5)(x−2)(x−5).

To find the solutions, set each factor equal to zero: x−2=0x – 2 = 0x−2=0 and x−5=0x – 5 = 0x−5=0. Solving these equations gives x=2x = 2x=2 and x=5x = 5x=5. These are the solutions to the polynomial equation.

Factorization helps simplify the polynomial, making it easier to find the solutions. By breaking the polynomial into factors, you can solve it more efficiently and understand the process of solving polynomial equations better.

The Role of Substitution in Polynomial Eqn Solving with SF

Substitution (SF) is a method used to solve polynomial equations by replacing variables with simpler expressions. This technique helps simplify the polynomial and makes it easier to solve.

For example, if you have the polynomial equation x2+2xy+y2=0x^2 + 2xy + y^2 = 0x2+2xy+y2=0, you can use substitution to simplify it. Let’s substitute x=yx = yx=y. The equation becomes y2+2y2+y2=0y^2 + 2y^2 + y^2 = 0y2+2y2+y2=0, which simplifies to 4y2=04y^2 = 04y2=0. Solving this gives y=0y = 0y=0. Substituting back, x=0x = 0x=0 as well.

Substitution helps in reducing the complexity of the polynomial equation, making it easier to solve. By replacing variables with simpler expressions, you can simplify the equation and find the solutions more efficiently.

How Factoring Works in Polynomial Eqn Solving with SF

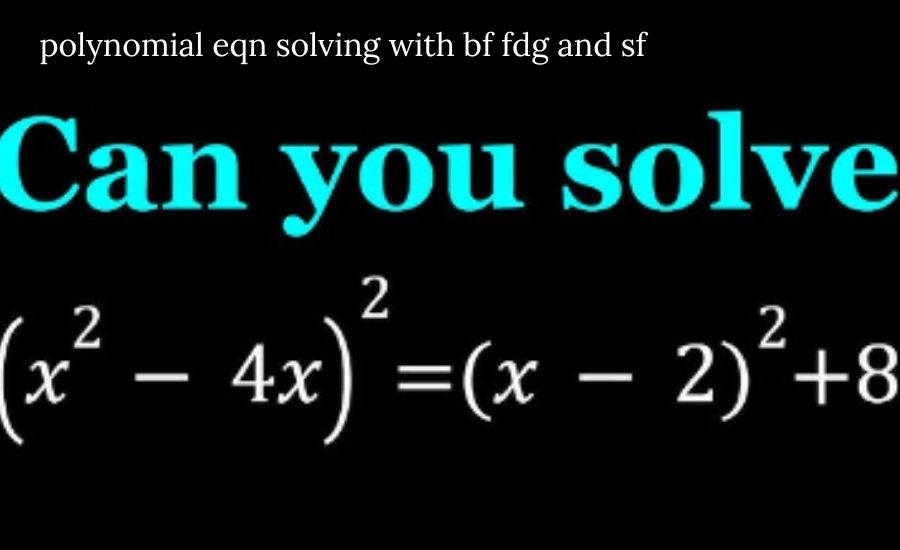
Factoring, as part of the Substitution and Factoring (SF) method, involves breaking down a polynomial into simpler factors. This process helps in solving the polynomial by reducing its complexity.

For instance, consider the polynomial x2−9x^2 – 9×2−9. To factor it, rewrite it as (x−3)(x+3)(x – 3)(x + 3)(x−3)(x+3). Now, you can solve the polynomial by setting each factor equal to zero: x−3=0x – 3 = 0x−3=0 and x+3=0x + 3 = 0x+3=0. This gives the solutions x=3x = 3x=3 and x=−3x = -3x=−3.

Factoring is an essential part of solving polynomials, especially when combined with substitution. By breaking the polynomial into factors, you can simplify the equation and solve it more efficiently.

Combining SF with Other Methods for Effective Polynomial Solving

Combining the Substitution and Factoring (SF) method with other solving techniques can be very effective for polynomial equations. For example, you might use substitution to simplify a polynomial and then apply factorization to solve it.

Let’s say you have a polynomial equation x3+6×2+11x+6x^3 + 6x^2 + 11x + 6×3+6×2+11x+6. Start by using substitution to simplify it. Substitute x=y−1x = y – 1x=y−1, which simplifies the polynomial. Next, factor the simplified polynomial into (x+1)(x+2)(x+3)(x + 1)(x + 2)(x + 3)(x+1)(x+2)(x+3). Finally, solve for xxx by setting each factor equal to zero.

Combining methods helps in solving more complex polynomial equations efficiently. By using substitution to simplify and factoring to solve, you can handle challenging problems more effectively.

Comparing BF, FDG, and SF in Polynomial Eqn Solving

When polynomial eqn solving with bf fdg and sf, different methods like Brute Force (BF), Factorization (FDG), and Substitution and Factoring (SF) have their own strengths and weaknesses. Comparing these methods helps in choosing the best approach for different types of polynomials.

Brute Force (BF) involves testing various values to find solutions. It’s simple but can be time-consuming for complex polynomials. Factorization (FDG) simplifies polynomials by breaking them into factors, which is efficient for quadratic and cubic polynomials. Substitution and Factoring (SF) help in simplifying polynomials by replacing variables and factoring, making it easier to solve.

Each method has its own advantages. BF is straightforward, FDG is efficient for certain types of polynomials, and SF helps in simplifying and solving more complex equations. Choosing the right method depends on the polynomial and the problem you’re trying to solve.

Common Challenges in Polynomial Eqn Solving with BF FDG and SF

Polynomial eqn solving with bf fdg and sf using methods like Brute Force (BF), Factorization (FDG), and Substitution and Factoring (SF) can come with its challenges. Understanding these common problems helps in finding solutions more effectively.

Brute Force (BF) can be time-consuming, especially for complex polynomials with many possible values to test. Factorization (FDG) requires correctly identifying factors, which can be tricky for higher-degree polynomials. Substitution and Factoring (SF) involve replacing variables and factoring, which might be confusing for some equations.

By being aware of these challenges, you can prepare better and use strategies to overcome them. For example, using a combination of methods might help in solving more complex equations more efficiently. Understanding these common issues will improve your problem-solving skills and help you tackle polynomial eqn solving with bf fdg and sf more effectively.

Don’t Skip: Sv sys-511r-m

Tips and Tricks for Mastering Polynomial Eqn Solving with BF FDG and SF

Mastering polynomial eqn solving with bf fdg and sf involves understanding and applying different methods effectively. Here are some tips and tricks to help you become proficient in using Brute Force (BF), Factorization (FDG), and Substitution and Factoring (SF).

For Brute Force (BF), start with simple values and check each one systematically. For Factorization (FDG), practice factoring different polynomials to become familiar with the process. With Substitution and Factoring (SF), focus on simplifying polynomials before factoring to make the solving process easier.

Additionally, combining methods can be very effective. For example, use substitution to simplify the polynomial first and then apply factorization. Regular practice and solving various types of polynomials will help you master these techniques and become more confident in polynomial eqn solving with bf fdg and sf.

Real-World Applications of Polynomial Eqn Solving with BF FDG and SF

Polynomial equations are not just academic exercises; they have real-world applications in various fields. Understanding how to solve them using methods like Brute Force (BF), Factorization (FDG), and Substitution and Factoring (SF) can be very useful in practical scenarios.

In engineering, polynomial eqn solving with bf fdg and sf are used to model different systems and processes. In computer science, algorithms often involve solving polynomial equations for optimization problems. Economics also uses polynomial eqn solving with bf fdg and sf to model financial systems and market trends.

By learning and applying these methods, you can solve complex problems in real-world situations. Understanding how polynomial equations fit into these fields helps in appreciating the importance of mastering these solving techniques.

Troubleshooting Polynomial Eqn Solving Issues Using BF FDG and SF

Solving polynomial equations using methods like Brute Force (BF), Factorization (FDG), and Substitution and Factoring (SF) can sometimes lead to issues. Troubleshooting these problems effectively will help you find solutions more efficiently.

For Brute Force (BF), ensure that you are testing a reasonable range of values and avoid missing potential solutions. With Factorization (FDG), double-check your factors to ensure accuracy and avoid mistakes. For Substitution and Factoring (SF), make sure that your substitutions are correct and that you’ve factored the polynomial correctly.

When encountering difficulties, revisiting the basics of each method and practicing with different problems can be helpful. Seeking additional resources or asking for help from peers or teachers can also improve your problem-solving skills. Effective troubleshooting will enhance your ability to solve polynomial equations and tackle more complex problems.

Conclusion

polynomial eqn solving with bf fdg and sf can be a fun and rewarding challenge. Whether you’re using Brute Force (BF), Factorization (FDG), or Substitution and Factoring (SF), each method has its own way of making tricky math problems easier. Brute Force involves trying out different answers until you find the right one. Factorization breaks down the equation into simpler parts. Substitution and Factoring simplify things by replacing parts of the equation with easier expressions.

By learning these methods, you’ll become more confident in solving polynomial equations. Remember, practice makes perfect, so keep working on different problems to get better. With these tools in your math toolbox, you’ll be able to tackle even the toughest polynomial equations with ease. Happy solving!

Rea More: Cute Besties Scarlett and Cookie Play Naughty Games

FAQs

Q: What is polynomial eqn solving with BF FDG and SF?
A: Polynomial eqn solving with BF FDG and SF (Brute Force), FDG (Factorization), (Substitution and Factoring) involves methods to find solutions to polynomial equations. BF tries different values to find the right answer, FDG breaks the equation into simpler factors, and SF uses substitution and factoring to simplify the problem.

Q: How does Brute Force (BF) work in polynomial equations?
A: Brute Force (BF) involves guessing possible solutions and checking if they work. You test different values to see if they satisfy the equation, which can be time-consuming but effective for simpler problems.

Q: What is Factorization (FDG) in polynomial equation solving?
A: Factorization (FDG) is the process of breaking down a polynomial equation into simpler components or factors. This makes it easier to solve because you deal with simpler equations that are easier to handle.

Q: How do Substitution and Factoring (SF) help in solving polynomials?
A: Substitution and Factoring (SF) involve replacing parts of the equation with simpler expressions and then factoring the result. This method simplifies the equation, making it easier to solve.

Q: Can these methods be used for all polynomial equations?
A: Yes, these methods can be applied to most polynomial equations. However, the complexity of the equation may make some methods more practical than others.

Q: What should I do if I can’t solve a polynomial equation using these methods?
A: If you have trouble, consider trying different methods, seeking help from a teacher or tutor, or using math software tools. Sometimes, combining methods or additional practice can also help.